[Godot] C# 实现环绕中心点旋转效果（普通+真实）

实现效果

普通旋转

真实旋转（使用开普勒方程式）

实现流程

场景搭建

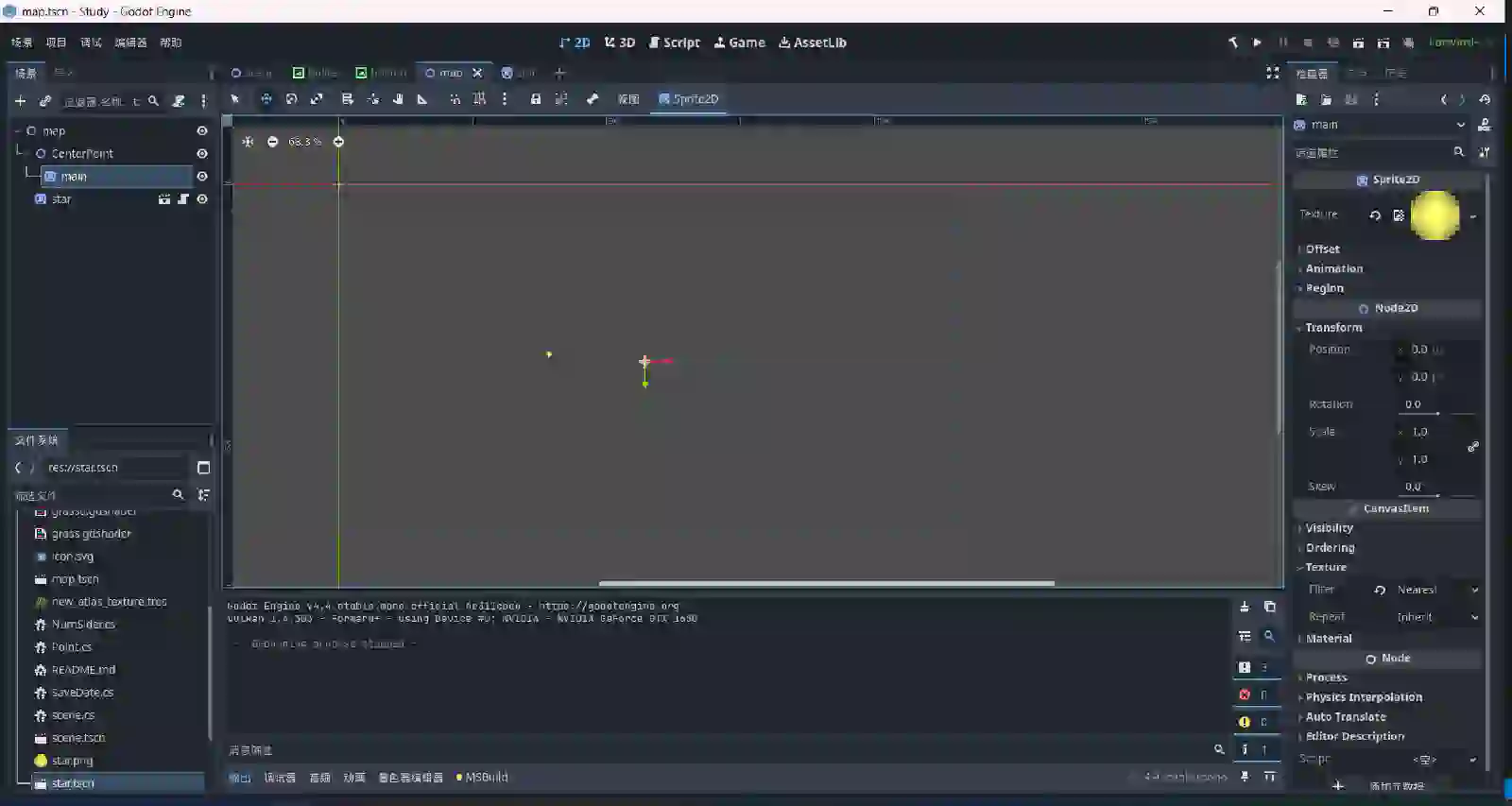
如图所见，主要的就是两个点，一个点作为 中心点 ，一个作为 旋转点 （当然你也可以添加更多旋转点）

普通旋转实现

给旋转点写脚本，下面是代码：

using Godot;
using System;
 
public partial class Point : Node2D
{
    [Export] public float RotationSpeed;    //旋转速度
    [Export] public float OrbitRadius;  //轨道半径
    [Export] public int Direction;
    //旋转方向，1为顺时针，-1为逆时针
 
    private Node2D centerPoint; //旋转中心
 
    private float angle;
 
    public override void _Ready()
    {
        centerPoint = GetNode<Node2D>("../CenterPoint"); //获取中心点
    }
 
    public override void _Process(double delta)
    {
        UpdatePosition((float)delta);
    }
 
    void UpdatePosition(float delta)
    {
        angle += Direction * RotationSpeed * (float)delta;
 
        float x = centerPoint.Position.X + OrbitRadius * Mathf.Cos(angle);
        float y = centerPoint.Position.Y + OrbitRadius * Mathf.Sin(angle);
        Position = new Vector2(x, y);
    }
 
}

按照自己的需要，在检查器里面填写数值

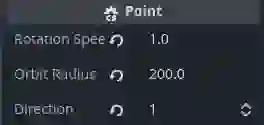
可以修改Direction来控制旋转方向

好了，我们运行场景看看

顺时针

逆时针

简单的旋转就实现了，大家之后可以按照自己的需求来写，接下来我们要实现更真实的旋转

真实旋转实现

要想实现更真实像太空中星星之间的旋转，需要用到 开普勒方程式

下面是脚本

using Godot;
using System;
 
public partial class Point : Node2D
{
    [Export] public float SemiMajorAxis = 100.0f;  // 半长轴
    [Export] public float Eccentricity = 0.5f;     // 轨道离心率
    [Export] public float OrbitalPeriod = 5.0f;    // 轨道周期（秒）
    [Export] public int Direction = 1;             // 方向，1=顺时针，-1=逆时针
 
    private Node2D centerPoint; 
    private float meanAnomaly;   // 平均近点角 M
    private float meanMotion;    // 平均角速度
    private const int Iterations = 5; // 计算偏近点角的迭代次数
 
    public override void _Ready()
    {
        // 获取同级的 CenterPoint
        centerPoint = GetNode<Node2D>("../CenterPoint"); 
    }
 
    public override void _Process(double delta)
    {
        UpdatePosition((float)delta);
    }
 
    void UpdatePosition(float delta)
    {
        meanMotion = 2 * Mathf.Pi / OrbitalPeriod; // 计算平均角速度
        // 更新平均近点角 M，并保持在 0 到 2π 之间
        meanAnomaly = (meanAnomaly + Direction * meanMotion * delta) % (2 * Mathf.Pi);
        if (meanAnomaly < 0) meanAnomaly += 2 * Mathf.Pi; // 确保 M 为正
 
        // 计算偏近点角 E（通过迭代求解开普勒方程）
        float eccentricAnomaly = SolveKepler(meanAnomaly, Eccentricity);
 
        // 计算真实轨道位置
        float trueAnomaly = 2 * Mathf.Atan2(
            Mathf.Sqrt(1 + Eccentricity) * Mathf.Sin(eccentricAnomaly / 2),
            Mathf.Sqrt(1 - Eccentricity) * Mathf.Cos(eccentricAnomaly / 2)
        );
 
        // 计算轨道半径（使用开普勒轨道方程）
        float orbitRadius = SemiMajorAxis * (1 - Eccentricity * Mathf.Cos(eccentricAnomaly));
 
        // 计算最终的 x, y 位置
        float x = centerPoint.Position.X + orbitRadius * Mathf.Cos(trueAnomaly);
        float y = centerPoint.Position.Y + orbitRadius * Mathf.Sin(trueAnomaly);
 
        Position = new Vector2(x, y);
    }
 
    // 迭代求解偏近点角 E（使用 Newton-Raphson 方法）
    private float SolveKepler(float M, float e)
    {
        float E = M; // 初始估计
        for (int i = 0; i < Iterations; i++)
        {
            E = E - (E - e * Mathf.Sin(E) - M) / (1 - e * Mathf.Cos(E));
        }
        return E;
    }
}

我们现在可以修改四个属性来确定这个旋转轨道

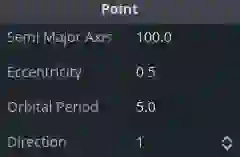
第一个是 轨道的大小 （长轴），第二个是 轨道的离心率 （-1~1，越接近0，越近似为一个圆），第三个是 轨道周期 （旋转一圈所需要的速度），第四个是 旋转方向

其他

我们可以加上旋转轨道，有两种实现方法，一种是自带的 _Draw函数 直接实时的画出来，另一种用 粒子系统 或者用 Line2D+shader 做一个拖尾，这里就不过多赘述了，至于更多的旋转点和卫星这种，大家可以根据自己的实际需求来处理，这里给大家看看我之前做的一个已经放弃的项目效果